표준편차를 n 대신 n-1 을 쓰는 이유
n으로 나누다가
대학에 오니 n-1로 나누는 것을 배웠다.
대체 왜????
그런 것일까에 대한 뚜렷한 해답을 알고 싶었다.
그 해결의 실마리는 바로...
1. Population 과 Sample의 차이
2. Population의 true mean 을 모른다는 사실 때문이었다.
자~! 차근 차근히 설명해 보자.
여기서 Population과 Sample의 차이를 알아야 한다.
Population은 말 그대로 통계적 사실을 얻고자 하는 대상 전부를 의미한다.
예를 들어 얻고자 하는 통계적 사실이
"2008년 대입 수험생의 하루 평균 공부 시간은?"
에 대한 사실을 얻고 싶다고 하자.
올해 대입 수험생이 55만 9천여명이라고 하니까
정확히 55만 9314명이라고 하면
Population = 55,9314 가 된다.
그런데 고3 수험생의 하루 평균 공부시간을 알고 싶다고 해서
55,9314 명의 사람 전부에게 전화를 걸어서
"몇시간 공부하세요?" 라고 물어볼수는 없는 일이다.
그래서 우리는 Sample을 추출한다.
Sample 을 추출하는 방식은 여러가지가 있지만
Random 하게 1000명을 추출했다고 해보자.
그러면 Sample = 1000 이 되는 것이다.
여기까지 얻게된 사실은
Population과 Sample은 다르고 만약 Population을 모두다~ 조사해서
평균과 분산을 구하면 n으로 나누는 것이 맞고
Sample을 추출하여 조사하면 n-1로 나눈다는 것이다.
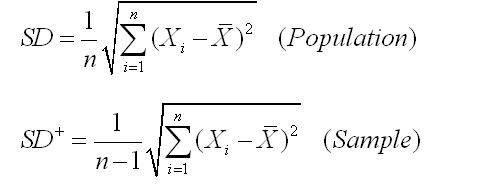
자~! 또다른 Key point는 지금 SD+에 있는
평균은 Sample의 평균이지
Population의 평균이 아니라는 사실이다.
그렇다면 왜 n-1로 나누는 것일까??
예를들어 설명해 보자.
알고싶은 사실이
"내 친구 12명중 아스날의 파브레가스의 플레이를 TV를 통해 본 적이 있는 사람의
평균과 표준 편차를 알고 싶다고 하자."
나는 귀찮지만 12명에게 직접 다 물어봐서 Population의 응답 결과를 다 안다고 가정하고
내가 아는 아주 친한 형 훈드리아누는 딱 한번 4명의 Sample을 통해
참값을 유추해 오차가 10 보다 작으면 아이스크림을 사주는 내기를 했다고 하자.
그래서 12명 중 4명을 Sampling 했다.
나의 결과
Population = 12
응답결과 = 0 0 0 0 0 0 1 1 1 1 1 1
평균 = 0.5 SD = 0.5 (평균과 표준 편차 모두 참값임)
훈's 결과
Sample = 4
응답결과 = 0 0 0 1
평균 = 0.25 SD = 0.433
얼레~ 표준편차 값이 참값에 비해 너무 작다.
그 이유가 바로 True mean 인 0.5를 사용하지 않고
Sample의 mean인 0.25를 사용하였기 때문이다.
그런데 여기서 SD+ 를 사용할 경우 SD+ = 0.5
Wow ice cream 얻어 먹을 수 있겠군.. ^^;
그러니까 n-1로 나누는 이유는
Population의 참 평균 값을 모르기 때문에 Sampling에서 생기는
오차를 조금이나마 키워 주기 위해서 n-1로 나누는 것이었군~!
이 결론이다.
(수학적으로는 unbiased estimator라고 해서 막 수식 전개한 내용이 있다.
휴~ 이 글 쓰는게 이렇게 어렵다니...
자신의 지식을 잘 설명해 놓은 블로거들이 대단하다고 느껴진다.
자료출처 : http://blog.naver.com/preciousbody?Redirect=Log&logNo=20058704671
분산과 표준편차를 구하는 공식에서 n-1을 사용하는데, n이 아닌 n-1로 나누는 이유는 무엇일까?
여기서 먼저 알려둘 것은 실제로 모집단에 대한 분산과 표준편차를 구할 때는 공식에서 n으로 나누어 주어야 한다는 것이다. n-1을 사용하는 것은 표본의 분산, 표준편차를 구할 때이다.
SPSS는 데이터 파일을 표본으로 가정하기 때문에 n-1을 사용한다. 쉽게 이해가 되겠지만, 표본크기가 커지면 n과 n-1의 차이는 실제로 없어진다. 단지 표본의 크기가 작을 때, 실제적인 차이가 발생하는 것이다.
n-1을 사용하는 이유는 표본의 분산이나 표준편차를 모집단의 분산이나 표준편차를 예측하는 추정치로 사용하려는 의도 때문이다. 표본의 크기가 작은 경우 표본의 분산이나 표준편차는 n을 사용할 경우, 모집단의 분산이나 표준편차를 작게 추정하는 경향을 보이기 때문이다. 좋은 추정치, 즉 불편추정치(unbiased estimate)를 만들기 위해 n-1을 사용한다고 할 수 있다.
...이 외에도 인터넷으로 찾아보아 보충하였습니다....
수학사랑 저널 2000 년 4 월호(20호) 에 실린 양인웅(fifit@mathlove.org) 선생님의 글을 소개해 드리겠습니다.
'분산(variance)' 은 평균을 가준점으로 자료들이 얼마나 퍼져 있는지를 재는 측도입니다. 평균을 원점으로 간주했을 때 각 관측값들의 상대적인 위치를 '편차(deviation)' 라고 부르며 '관측값-평균' 으로 정의됩니다.
그런데 편차의 합은 항상 '0' 이 되기 때문에 편차의 절대값을 취하거나 제곱을 합니다. 편차에 절대값을 취한 것의 평균을 '평균절대편차(mean absolute deviation)' 라고 부르며 제곱한 것의평균을 '평균제곱편차(mean squared deviation)' 라고 부릅니다.
그런데 평균절대편차는 계산의 어려움때문에 상당히 제한적으로 사용되고 평균제곱편차도 실제 자료분석을 할 때에는 잘 사용되지 않습니다.
자료분석을 할 때 일반적으로 사용하는 분산에서는 제곱 편차의 합을 'n-1' 로 나눈 값을 사용합니다. 이것을 '불편분산(unbiased variance)' 이라고도 합니다. 그러면 왜 'n-1' 로 나눈 값을 사용하는지 궁금하죠? 그것은 바로 '자유도(degree of freedon)' 때문입니다.
분산을 계산할 때에는 반드시 평균을 먼저 계산하게 되고 평균을 알고 나면, 원래 자료 중의 한 값을 잃어도 정보는 전혀 손실되지 않습니다. 다시 말해 평균을 알고 나면 자료 중에 어느 한 값은 항상 잉여정보가 되고 따라서 자유도는 '관측수-1' 이 됩니다.
따라서 평균을 계산할 때에는 자유도가 '관측수' 이고, 분산을 계산할 때는 자유도가 '관측수-1' 이 됩니다.
그런데 관측수가 커지면 관측수를 사용하든 자유도를 사용하든 별차이가 생기지 않습니다. 다만 자유도 개념을 기초로 한 분산이 관측수를 기초로 만든 평균제곱편차보다 수리적으로 우월한 점이 있기 때문에 통계학에서는 주로 자유도를 이용한 분산을 사용하고 학교에서는 간편하게 관측수를 이용한 평균제곱편차를 분산으로 사용하고 있을 뿐입니다.//
자료출처 : http://cafe.naver.com/sejongin.cafe?iframe_url=/ArticleRead.nhn%3Farticleid=194&
http://gall.dcinside.com/list.php?id=probability&no=1932
표준편차에서 분모를 n대신 n-1로 하는지~~
아주 자세히~~
좀 알려주세요~~~~~
음, 고등학교 이후 통계를 처음 접하는 비전공분들이 주로 묻는 질문이라고 생각됩니다. 이곳에 쓴적이 있었나 가물가물해서 다시 집어보면, 음, 개념적으로 일단 한번 보면, 일단 모분산과 표본분산의 차이에 대한 감이 있어야 겠지요. 모분산은 쉽게, 말그대로 모집단에 대한 분산이며 모집단의 모든값들에 대해 계산된 값이겠지요. 표본분산은 모집단의 부분집합인 표본에 대한 분산이겠고요. 그럼 이제 머리속에 정규분포 하나를 그려보시길요. 이제 거기서 10개 정도의 표본을 뽑아 봅니다. 이때 정규분포의 특징상 평균 부분에서 많이 뽑히겠지요?. 그렇다면 이렇게 가운데 부근에서 많이 뽑힌 표본분산값들과, 모집단의 각 값들을 고려한 모분산을 비교해보면 일반적으로 표본분산이 더 작겠지요. 이것은 한 문장으로 정리하면
"표본분산은 모분산보다 작아질려는 성질이 있다'라는 말로 요약을 할 수 있겠지요. 이제 좋은 표본분산에 대한 것을 한번 살펴봅니다. 좋은 기준 중 하나는 표본분산의 "기대값"이 모분산이 되느냐? 라는 것이겠지요. 그런데 앞에서도 살펴봤듯이 , N으로 나눈 표본분산은 일반적으로 모분산보다 작아지려는 경향이 있기 때문에 그 기대값이 모분산을 지향하지 않게됩니다. 그렇다면 어떻게 하면 표본분산의 기대값이 모분산이 될것인가에 대해 수리적으로 계산을 한것이 N이 아닌 N-1 나눈 표본분산이 됩니다. 즉 N-1로 나눈 표본분산의 기대값이 모분산이 나오게 됩니다.
여기까지 이해하셨으면, 위의 이야기들은 이제 날려버리시고 깔끔하게 " "불편추정량"이 되기 위하여 n-1로 나눈 표본분산을 사용한다" 정도로 요약해서 기억하시면 별 무리가 없을듯 합니다. (불편추정량의 자세한 개념은 어느 통계학책이나 나와있을테니 필요시 참고하시길요, 표본표준편차는 표본분산의 양의 제곱근이니 별 다른 설명은 하지 않겠고요)
'통계' 카테고리의 다른 글
| 통계적으로 유의미한 결과는 얼마나 유의미할까 (0) | 2016.05.29 |
|---|---|
| 250주년 베이즈 정리 (0) | 2013.07.25 |
| 미주 한인 인구는? (0) | 2011.09.13 |